Support Vector Machines

引言

内核方法是模式分析中非常有用的算法，其中最著名的一个是支持向量机SVM

工程师在于合理使用你所拥有的toolkit

相关代码

本文要点

1.Please explain Support Vector Machines (SVM) like I am a 5 year old - Feynman Technique

2.kernel trick

一、术语解释

1.1 what is support vector?

从名词解释角度来看：

“支持向量机”为偏正结构，所以分别解释“支持向量”和“机”

（1） “机” —— Classification Machine，分类器，这个没啥好说的了。Machine means system.

（2） “支持向量” —— Support Vector.在maximum margin上的这些点就叫支持向量，我想补充的是为啥这些点就叫支持向量，因为最后的classification machine的表达式里只含用这些“支持向量”的信息，而与其他数据点无关：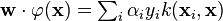

这个表达式中，只有支持向量的系数不等于0

引用Wiki：

• classification problem
• support vector can be used to define decision boundary.

support vector本质是向量，而这些向量却起着很重要的作用，如果做分类，他们就是离分界线最近的向量。也就是说分界面是靠这些向量确定的，他们支撑着分类面。

1.2 点积

投影 —— to a number : represents how much they're pointing in the same direction

表示向量指向同一方向的程度（相似度的度量）

the projection of one of those onto the other

在数学中，数量积（dot product; scalar product，也称为点积）是接受在实数R上的两个向量并返回一个实数值标量的二元运算。

它是欧几里得空间的标准内积。

两个向量$ a = [a1, a2,…, an] $ 和 $ b = [b1, b2,…, bn] $ 的点积定义为：

$ a·b=a_1b_1+a_2b_2+……+a_nb_n $

使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：

$ a·b=a^T*b $ ，这里的 \(a^T\) 指示矩阵 \(a\) 的转置。

\(X^T * y\) : the projection of y onto x.

投影到第三个维度上，并且找到一个分隔超平面

1.4 核技巧 kernel trick

本质：高维攻击低维

what is the kernal？

the kernel is the function itself ——represent similarity

1.5 Mercer Condition

直观解释：

核函数要能够作为一种距离或一种相似性，它不能是一个与各个点都不相关的任意条件。

1.6 小结

• margins ~ generalization & overfitting
• optimization problem for finding max margins : turn out to be quadratic programming.
• the dual of the quadratic problem. (二次规划问题的对偶)
• support vectors
• kernel trick ： project the data into a higher dimension sapce
• X^T y generalize it to a generic similarity function K(X,y)
• domain knowledge
• Mercer Condition

二、 Explain (SVM) like I am a 5 year old

深入浅出 ，可谓是Feynman Technique的经典实例。

整理参考自

@Han Oliver@Linglai Li 前辈们的解释让人受益许多。

正好最近自己学习机器学习，看到reddit上 Please explain Support Vector Machines (SVM) like I am a 5 year old 的帖子，一个字赞！于是整理一下和大家分享。(如有错欢迎指教！)

什么是SVM?

当然首先看一下wiki.

Support Vector Machines are learning models used for classification: which individuals in a population belong where? So… how do SVM and the mysterious “kernel” work?

好吧，故事是这样子的：

在很久以前的情人节，大侠要去救他的爱人，但魔鬼和他玩了一个游戏。

魔鬼在桌子上似乎有规律放了两种颜色的球，说：“你用一根棍分开它们？要求：尽量在放更多球之后，仍然适用。”

于是大侠这样放，干的不错？

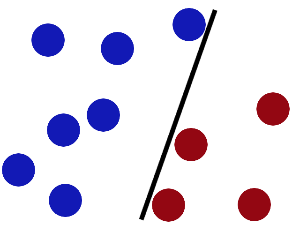
然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营。

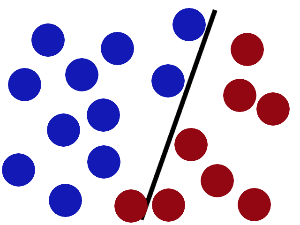
SVM就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙。

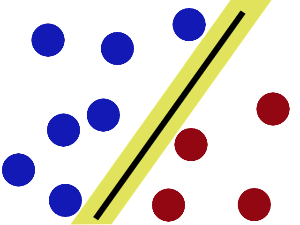
现在即使魔鬼放了更多的球，棍仍然是一个好的分界线。

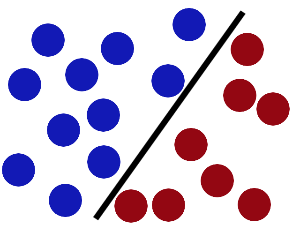
然后，在SVM 工具箱中有另一个更加重要的trick。 魔鬼看到大侠已经学会了一个trick，于是魔鬼给了大侠一个新的挑战。

现在，大侠没有棍可以很好帮他分开两种球了，现在怎么办呢？当然像所有武侠片中一样大侠桌子一拍，球飞到空中。然后，凭借大侠的轻功，大侠抓起一张纸，插到了两种球的中间。

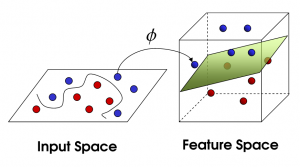
现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了。

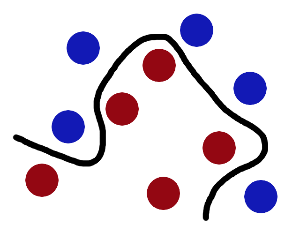
再之后，无聊的大人们，把这些球叫做 「data」，把棍子 叫做 「classifier」 , 最大间隙trick 叫做「optimization」， 拍桌子叫做kernelling」, 那张纸叫做「hyperplane」

图片来源：

直观感受看：https://www.youtube.com/watch?v=3liCbRZPrZA

作者：简之

链接：https://www.zhihu.com/question/21094489/answer/86273196

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

三、关于SVM的数学理解

大部分图源自 台大 林轩田老师 的讲义。

内容大概分为以下几个部分。

• 传统的SVM：最大间隔分类器

• SVM的优缺点

• SVM的第一种变形：软间隔分类器

• SVM的第二种变形：kernel method

• kernel，不止限于SVM

----------我是开始的分割线---------------

1. SVM：最大间隔分类器

回想一下所谓感知机：

感知机算法（PLA）可以找到一条线，把右图中的x和o分开。但是在使用时，往往会存在下面这样尴尬的情况：

这三条线都能成功的分开训练集中的点。但人类的直观感觉，第三种作为分类边界似乎更加‘稳妥一些’。 这种口语化的描述转化为数学语言，就是，我们希望寻找一条线，在能正确分类的同时，与数据点的分隔距离（margin）尽量的大。

如果真的去测量一下margin，就会得到下图：

最右面的图，确实是具有最大间隔的。而支持向量机，就是可以返回 margin最大的分隔直线 的一种分类算法。

SVM中的优化问题可以写成： ，

求解细节会用到凸优化，这里不再重复，但是我认为 这个过程中有一个 细节是必须要注意到的，就是转化为对偶问题后，待优化函数的形式，和最后表达式的样子：

上述优化问题的对偶问题长成这样：

（z就是x，我也不知道为啥林轩田换符号了）

而最终的返回结果长成这个样子

具体的推导可以不费力去搞懂，但里面有一点必须要格外留意，即只有数据点之间的内积会出现在最终的表达式里。 这一点与最终理解kernel息息相关。

2. svm的优缺点

SVM的优点是，返回的分割直线满足margin最大的条件，所以是一个robust的解。而且虽然上面因为没有具体写出推导过程所以这么说比较突兀，SVM对数据点的依赖 是稀疏的 ，只有少量支持向量对最终结果有贡献。

传统的SVM的缺点也很明显。首先SVM的优化问题比较复杂，不仅人难以理解，写起程序来也比较复杂，必须要用到Sequential minimal optimization（SMO）。其次，传统的SVM只能处理线性可分的问题，并且对数据中的噪音也很敏感，因此我们必要对算法进行改造。

3. SVM 的第一种变形：软间隔SVM

有时数据集大概还是线性可分的，只是存在一些噪音，比如下图：

，对于这种问题，我们的处理方式是 允许SVM犯一点错 。 这样的思想就产生了 Soft-Margin SVM 算法。

软间隔svm的优化问题大概长成这样：

第一项 $ \frac{1}{2}\omega^T\omega$ 代表我们希望间隔最大

而第二项中引入了松弛变量 \(\xi\) 代表我们在要求数据点满足约束的同时，也允许有一些异常点存在，他们或者分类错了，或者只是出现在了绿色的带状禁区里面。 而参数C就控制着二者的权衡。这就是sklearn中 正则化系数C的起源。

引入正则化之后，SVM对数据中的噪音不再敏感。可以更好的处理线性分类问题。

4. SVM的第二种变形： kernel method

有事数据集根本就不是线性可分问题，比如下图：

，这样的问题再搞正则项也没用，这时我们需要一种新的思想： 升维。

升维的思想简单说来就是：在原来feature的基础上人为的构造一些新的feature，在更高维度的空间里，原来不线性可分的问题就会变成线性可分的问题，就又可以用svm了。

相关的讨论论坛上已经有好多，我再这儿搬运一个帖子，http://www.zhihu.com/question/30371867，对高维空间里的线性可分来个直观感受。

升维的思想确实很漂亮，但是现实往往是很骨感的：如果对不同的数据集，每次都要寻找一个合适的函数，来把低维空间中的点x映射到高维空间中去是一件很困难的事情。

但是回想一下svm里的最终表达式，其实具体的表达式并不在最终结果里出现，出现的只有内积 \(<f(x_i),f(x_j)>\)。如果有办法直接算出高维空间中的新内积，不就不需要费力去构造了吗？

Kernel method正是基于这一思想的技巧。我们可以把kernel想象成 \(k(x_i,x_j) = <f(x_i),f(x_j)>\)，然后不去操心\(f（x）\)，而是尝试不同的kernel function就可以了。通常使用的kernel 有：

• linear kernel（其实就是不用kernel不升维）

• Polynomial Kernel

• Gaussian Kernel（sklearn里叫rbf kernel）

当你选用kernel时，升维已经自动做好了，所以在调用sklearn中带kernel的svm时才会各种奇形怪状的分类边界。

这里有一种kernel比较特别，高斯核。高斯核对应的映射f（x）是可以反算出来的，结果证明是 无穷维。 有兴趣的同学可以看一下下面的推导。

我想看到这里各位同学应该能理解为什么 svm with rbf kernel会这么强大，因为在选用rbf kernel时，数据已经被映射到了无穷维的空间中去，从而保证数据一定是线性可分的。

5. kernel，不止限于SVM

事实上，SVM这一节里面最重要的思想倒不是SVM本身，而是kernel。 Kernel提供了一种在 不写出具体映射表达式的情况下，计算数据内积的方法。 原则上说，但凡是需要计算内积的算法，都可以使用kernel trick，而不仅仅局限于svm。

我现在脑子里有的一个例子就是 带kernel的特征筛选算法 Lasso. 附上一篇paper的链接。

http://cs.brown.edu/~ls/Publications/nc2014yamada.pdf55

----------结束的分割线-----------

参考链接

1.

2.

3.